【菜鸟成长记】20岁后，我在机械的每一天

黑森林的鹿

hai9053 发表于 2016-2-19 14:22
羡慕楼，年轻，学校好，平台好，可以有很多选择，加油！！！

. Q% v+ P4 v, n1 g1 B真的？谢谢！一定好好努力，珍惜拥有的条件！

黑森林的鹿

【20160220】机械原理|机构的结构分析

平面机构的自由度基本计算公式
$ Y: }! W7 V+ U; r$ t8 s  N
* o  Q  B  a5 s7 @系统自由度F=所有运动构件的自由度-系统损失的自由度
2 e$ o; q+ R; `  Q, h- CF=3(N-1)-(3g-Σfi)=3(N-g-1)+Σfi
系统自由度F=所有运动构件的自由度-所有运动副的约束度
F=3(N-1)-Σci
进一步考虑高副和低副的差异(平面中，低副引入2个约束，高副引入1个约束)，可简化为
F=3(N-1)-(2PL+PH)
! a: T0 d6 H5 O8 x8 F* I& q, g
8 ~8 z# r% v: _7 C应用

! |4 c1 v7 N4 hF=3(6-1)-(2×7)=1
$ u& o6 r9 V. C/ r1 i: j* x, h
# I- r6 h5 C7 C+ a# j
' [/ R1 }5 V9 I! ZF=3(8-1)-(2×10)=1
% U! f! Y) q8 t

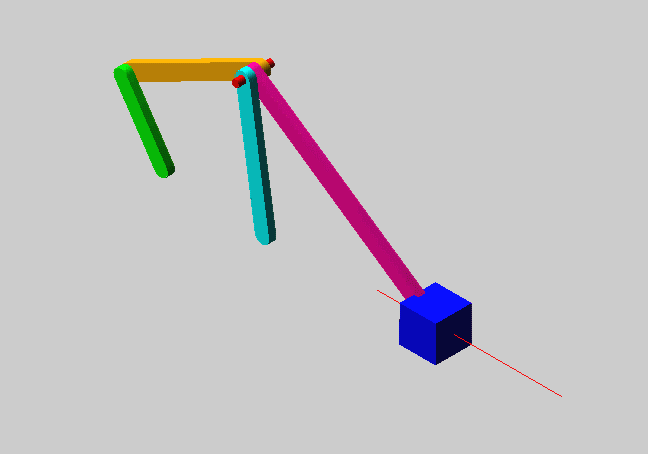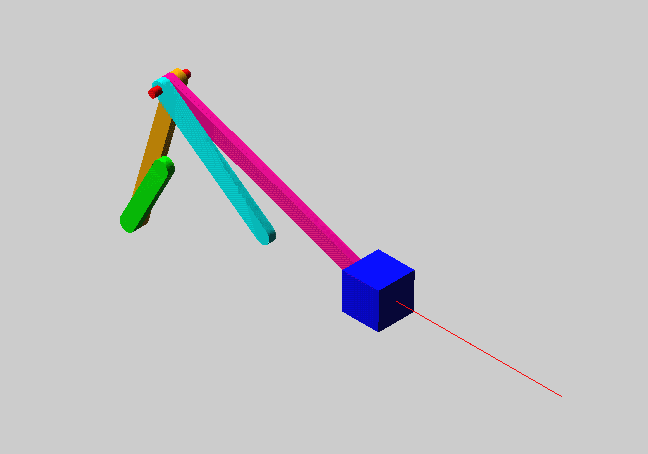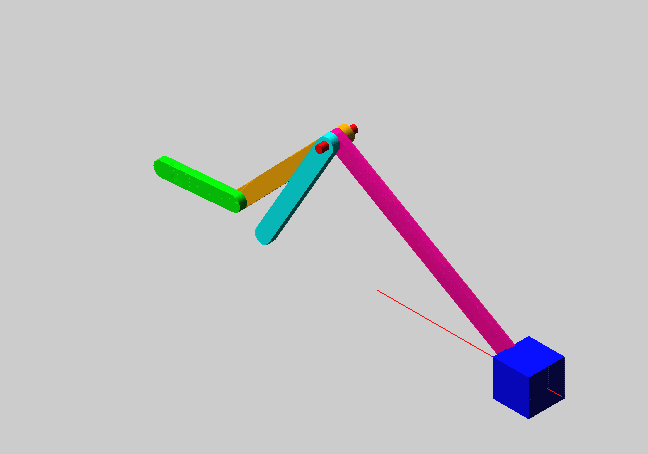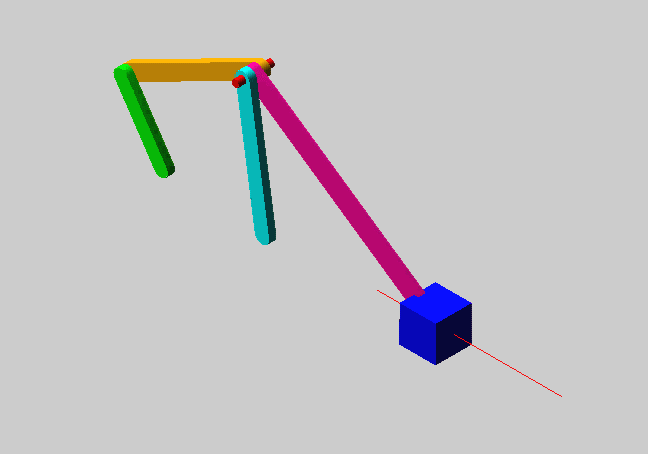
  W' V0 S/ I. Z4 \9 wF=3(6-1)-(2×7)=1
. L" J8 e; W2 t, e
局部自由度(idle DOF , passive DOF)又称冗余自由度，指机构中某些构件具有局部的，并且不影响其他构件运动的自由度。
& N8 @% C5 O8 N" n4 j, z& w7 s5 g
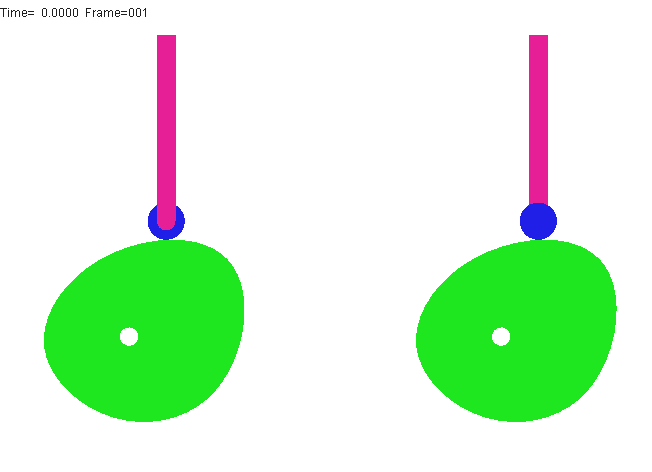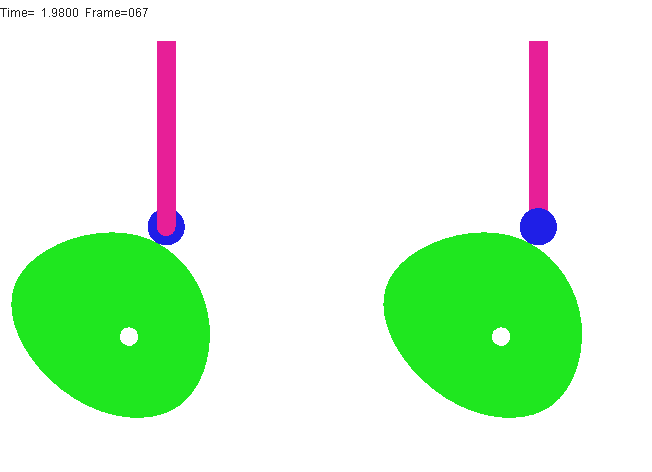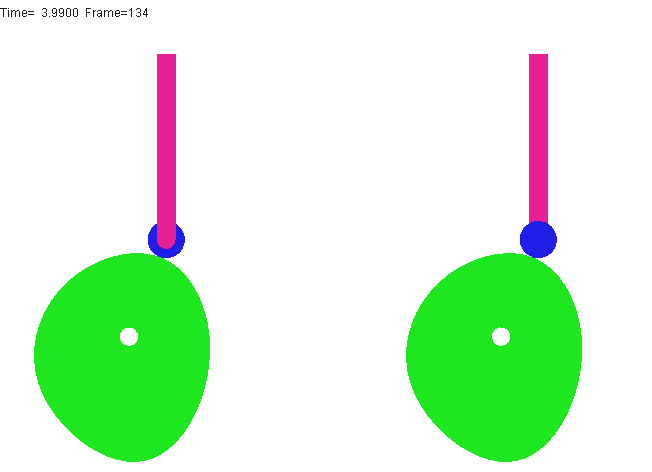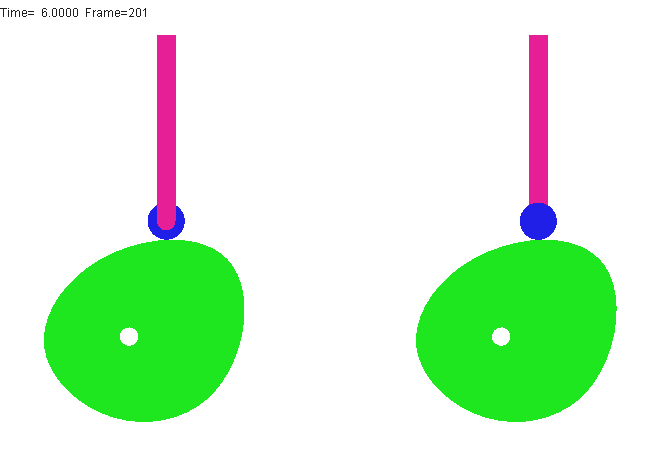
) u1 Q! f  c' G如图滚子推杆凸轮机构中，为减少高副元素的磨损，在推杆及凸轮间装了一个滚子，滚子与从动件为转动副连接，相对其有一个转动自由度，但滚子绕自身轴线的转动为局部的转动，并不影响其他构件的运动，因而它只是一种局部自由度。计算机构自由度时，应将局部自由度减去。则
. b' l4 B3 N% _* C2 EF=3×3-(2×3+1)-1=1
* R6 Q" ?, R' S& p* j3 W* ^还可将滚子与从动件视为一体：
# c! E5 y3 ^! N0 ^$ \F=3×2-(2×2+1)=1
* ]8 g7 {$ w2 h0 H
% a6 Q; a, e: j4 O$ L  F, `" m/ M/ c

の小南灬

楼主北理工的，建议多向北航 @十九子 女侠学习。

. G$ r" \& w3 Y) Y# D$ z. gmyth2000 百度贴吧她是大吧。

黑森林的鹿

【20160221】机械原理|机构的结构分析
/ S8 Z9 l: I7 z5 d5 Q. m/ V0 z
3 I: d4 M* X0 J$ u公共约束
' @' |2 B# |0 i/ N; A# d! w4 z
1 D& X3 Y9 }- P( U7 e7 x如图斜面机构，自由度F=3×2-2×3=0，但该机构可动。

: p: C4 U3 f. E' f解释：由于该机构为完全由移动副组成的平面机构，它的两个运动构件被限制在只能在一个平面内移动，故机构的公共运动空间维数(通常用d表示，即机构的阶数)不再是3而是2。
F=2×2-1×3=1
- C' o4 u* p, [
为此引入新概念——公共约束(common constraint)，即机构中所有构件均受到的共同约束。机构的阶数与机构的公共约束数(通常用λ表示)之间满足：
d+λ=6
9 n" n" D4 e7 ?/ S- _

$ B; d  C+ W* P5 t

黑森林的鹿

の小南灬 发表于 2016-2-20 15:33
楼主北理工的，建议多向北航 @十九子 女侠学习。
8 Z6 Y5 z" o/ B; ]1 U- }
myth2000 百度贴吧她是大吧。

感谢推荐！PS女王头像赞~Elsa真爱啊︿(￣︶￣)︿
4 F6 }6 E. Y) a; F, M

沧海一粟@only

MARK!

醉到疯癫

想当年我傻逼似的，大一的时候放假带书回家，然而一点也木有看。眨眼好几年，真是往事不堪回首啊。。。。楼主好样的，加油吧。

黑森林的鹿

【20160222】机械原理|机构的结构分析

& y) i  {$ T" Z, ]4 j+ H5 a& P冗余约束
- [( n3 i" L2 I& T
6 l# U/ O" _3 G. x) u2 e冗余约束(redundant constraint，虚约束)指在机构中，有些运动副所带入的约束对机构运动起重复约束作用。根据几何条件的不同，可分为4类：
+ [& M6 Q. @& u+ N& M+ Q# Y
1）两个构件直接接触而构成多个运动副。典型情况：
①两构件在多处接触构成移动副，且各移动副导路中心线平行或重合，则只能算作一个移动副，其余的都是冗余约束；
- _; g3 @4 c5 Y' h②两构件在多处配合组成转动副，且各转动副轴线重合，则只能算作一个转动副，其余的都是冗余约束；
③两构件在多处接触构成平面高副，且各接触点出的公法线重合或接触点的距离始终保持不变，则只能算作一个高副，其余的都是冗余约束。

2）如果将机构的某个运动副拆开，机构被拆开的两部分在原连接点的运动轨迹仍相互重合，则产生冗余约束。如图的椭圆仪机构即属此类。
2 z1 m; e3 w2 o- T1 m6 y7 E; ]
# R' w, V' g6 j5 s/ B/ R- @3）在机构运动过程中，如果某两构件上两点之间的距离始终保持不变，那么若将此两点以构件相连，则由此而引入的约束必为冗余约束。

4）机构中对运动不起作用的对称部分也是冗余约束。如图轮系即属此类。

注：都是在特定的几何条件下出现的，如果几何条件不满足，就是有效约束了。机械设计中冗余约束往往是根据实际需要采用的，如增强支承刚度，或改善受力，或传递较大功率等，只是计算自由度时应去除冗余约束。
如图机构自由度：F=3×6-(2×8+1)=1

公共约束与冗余约束统称过约束(overconstraint)，含有过约束的机构称为过约束机构(overconstraint mechanism)。
. X3 G3 }9 g; ~
( O6 R8 b/ [( S

黑森林的鹿

沧海一粟@only 发表于 2016-2-21 17:15
1 I1 ^  |! p& k$ }+ aMARK!

不敢不敢，个人学习记录而已，基础中的基础，无甚可观……动画嘛，不是自己做的，在网上找的还没那么厉害！
/ ^' j0 f, R& j7 S

黑森林的鹿

醉到疯癫 发表于 2016-2-21 17:29
想当年我傻逼似的，大一的时候放假带书回家，然而一点也木有看。眨眼好几年，真是往事不堪回首啊。。。。楼 ...

% i/ v" L: w6 D6 C) e) e' H& t哈哈！以前的假期我也这么过的！这次就怕再那样，才选了这么个方式监督自己呐！其实也没必要纠结带回的书看了多少，只要自问做了想做的事就好了！一起加油！
' G& v* [. }% }1 O$ y5 S- V