【20160223】机械原理|机构的结构分析
0 A" o5 `/ Z4 l. t
0 N# i8 p2 t6 w9 ]; m6 t一般空间机构的自由度计算公式
/ {+ b. e2 f: n% s* j
8 ?( g- G: M0 V6 U若在三维空间有N个完全不受约束的物体,并选择其中一个为固定参照物,这时每个物体相对参照物都有6个自由度若将所有物体之间用运动副连接起来,并选定其中一个构件为机架便构成了一个空间机构。该机构中含有N-1个或n个活动构件,连接构件的运动副用来限制构件间的相对运动。则. W! {% ^, ] N- F3 ?; {8 q
F=6(N-1)-(5f5+4f4+3f3+2f2+f1)=6(N-1)-Σifi=6n-Σifi
& O; r# P& P y. K更普遍的表达形式是格鲁巴-库兹巴赫[GrüblerßKutzbach(G-K)]公式,即1 a4 t8 b# q0 l( m. Q
F=d(N-1)-Σ(d-fi)=d(N-g-1)+Σfi* v% @* ^! _3 H" Q
式中g为运动副数。
: e$ i% f2 v9 `( _" y2 {. F2 z" o% B' D! P3 u b" J( y! }
单闭环:构件数等于运动副数,即g=N& d# x7 y3 G+ h, k; j6 z+ s3 j
若在一个单闭环中加上一条两端都有运动副的开链,则可形成另一闭环,这时增加的运动副数比增加的构件数多1,即每增加一个独立的环路,增加的运动副总数为g,而增加的构件数为g+1,这样当环路增加到L时,所增加的运动副数比所增加的构件数多L-1,即g-N=L-1,或L=g-N+1。
0 `' J9 Z- [% B6 S% A; N5 g3 U
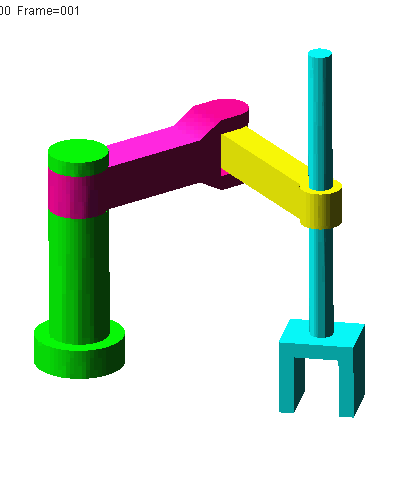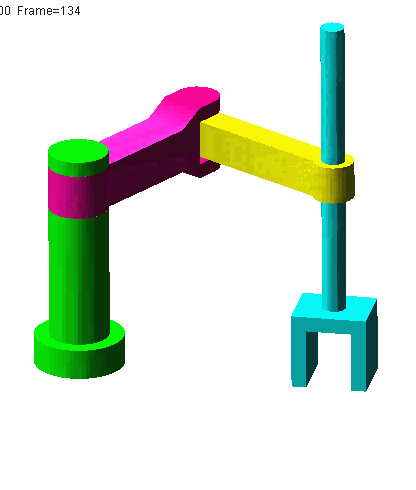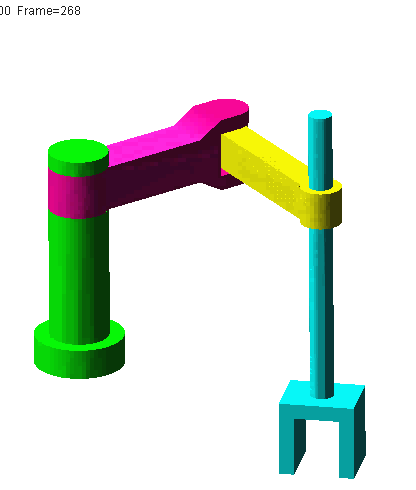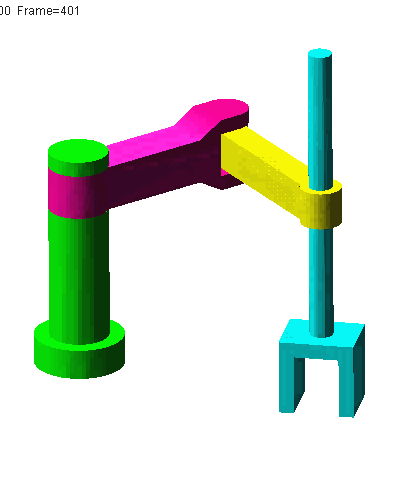
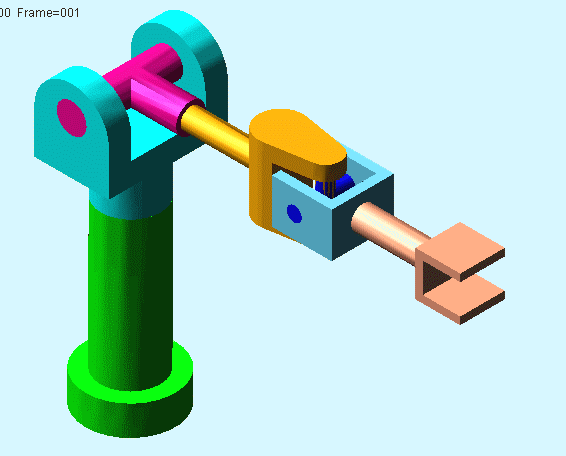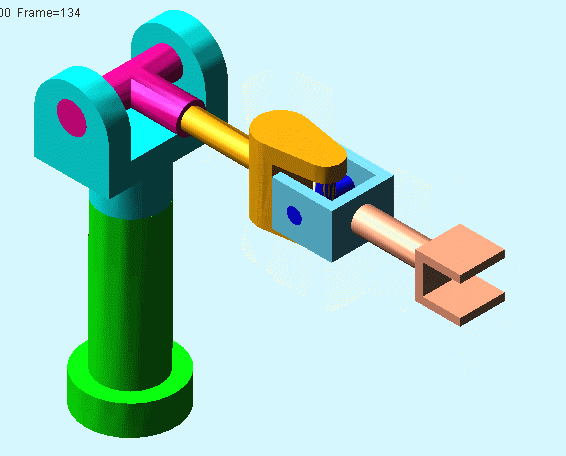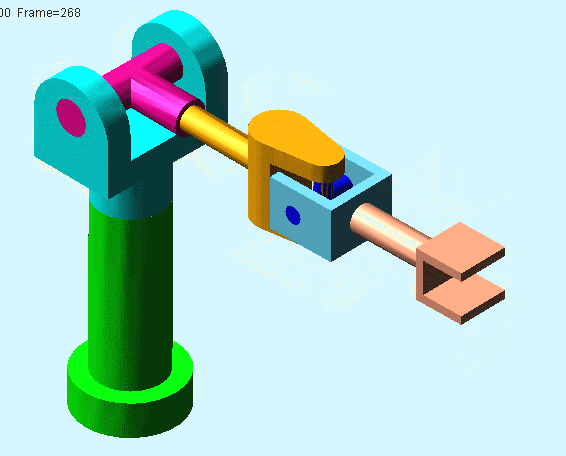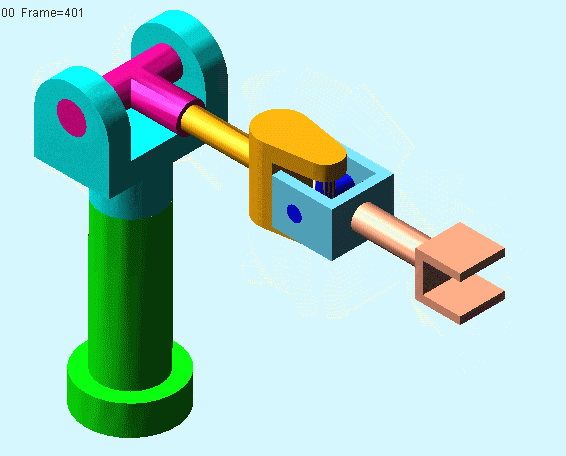
; @, M' \6 Q' @% W& q" L①平面关节型机器人,又称SCARA机器人(Selective Compliance Assembly Robot Arm)。, f" c1 B2 a7 d6 c: @( B6 k: B R% O
N=5,g=4,Σfi=4,F=6(N-g-1)+Σfi=4
. n o" j) t# h: h7 W) G
1
 " t. b3 a6 F1 A t% r
" t. b3 a6 F1 A t% r
②STANFORD机器人0 r1 d6 {) X: s+ ?( F6 S8 X1 z
N=7,g=6,Σfi=6,F=F=6(N-g-1)+Σfi=6
7 a @: t; P0 [5 h6 P& l0 P
2
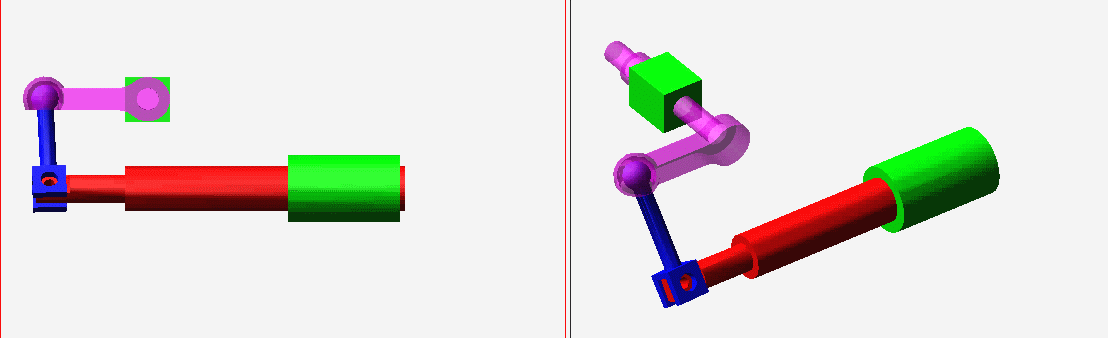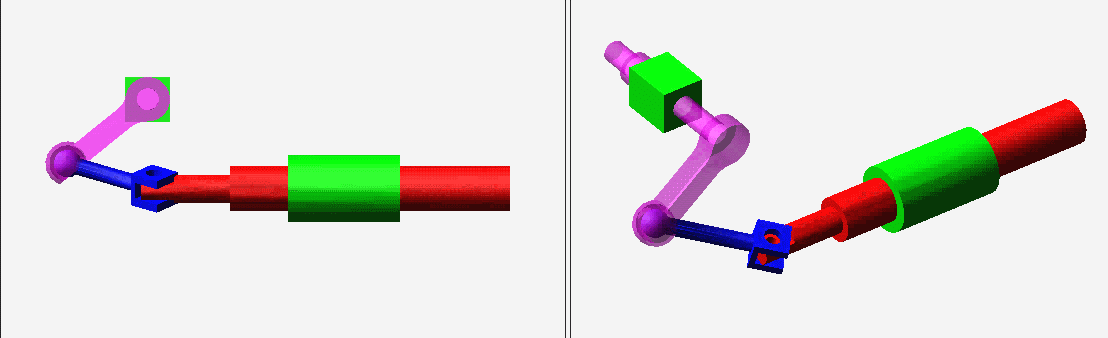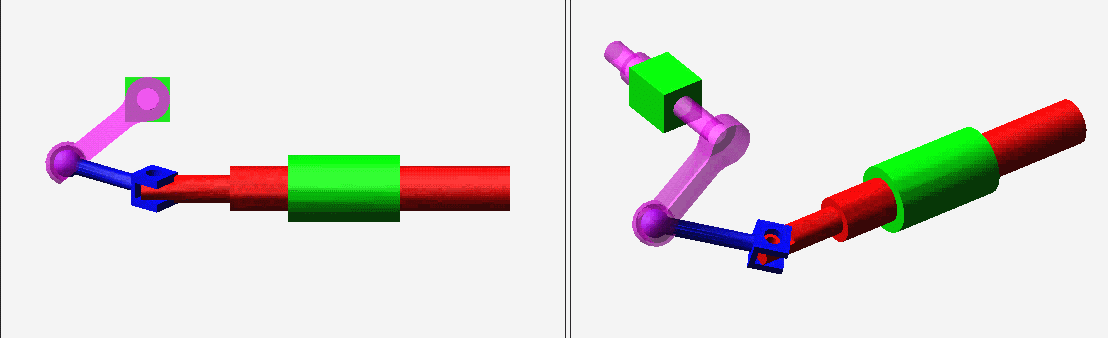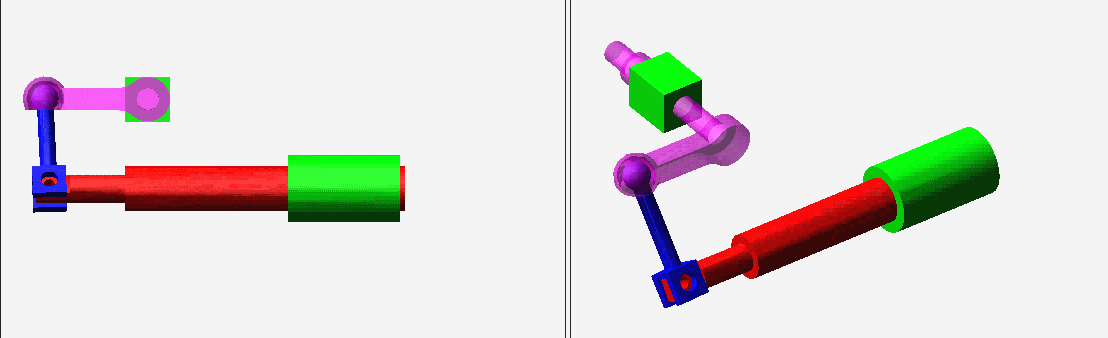
9 {3 g% c) E. n③自动驾驶仪操纵装置内的空间四杆机构。5 M- [0 [5 j, O ^) O+ X
N=4,g=4,Σfi=7,F=6(N-g-1)+Σfi=1
2 v4 c0 N3 `, _/ R o# N
3
/ z; {: @1 F+ I b5 E+ `
- E( f. z7 I0 u2 z甜啦噜这帖居然被鹰大推荐了!好激动好激动……坚持不易,坚持学习质量更不易。目前只是尽力做好第一步,没想到就得到了这么多的关注和支持!感谢各位!
( v! i7 w6 d, @) c2 a3 Z |