本帖最后由 黑森林的鹿 于 2016-2-24 10:12 编辑 2 L' O* J* A% l$ \* h3 T/ A/ a
( t/ G) u6 x# H7 F+ j9 _; |
【20160224】机械原理|机构的结构分析
5 X8 E5 g* x# W" o( \& k6 D3 {
$ z' C8 U2 D; F一般空间机构的自由度计算公式
: q6 ?) F, K1 w! e* t- A! Z d. k/ q( b! {
不满足G-K公式的情况:
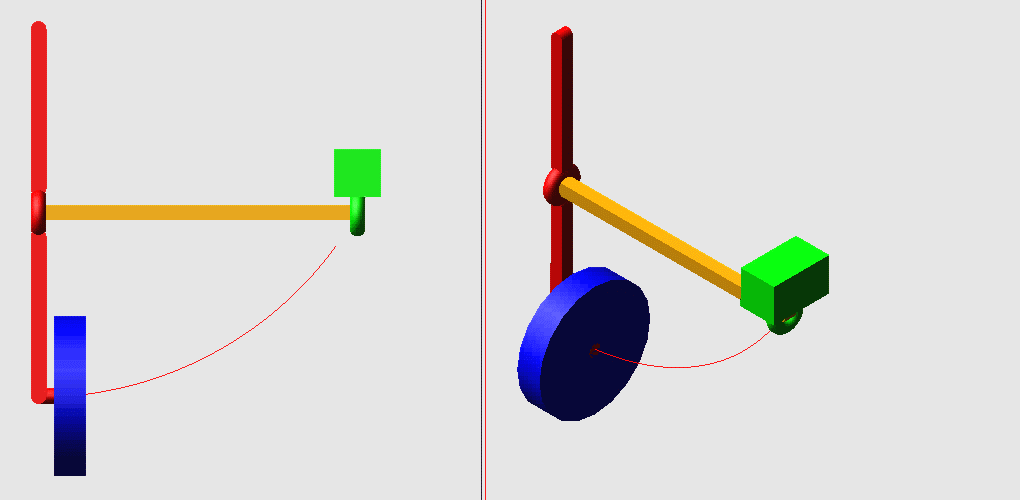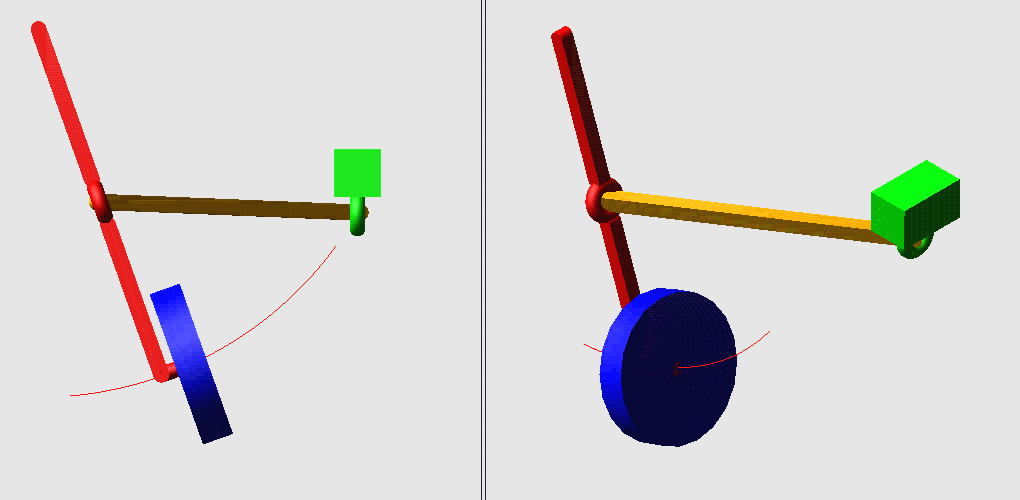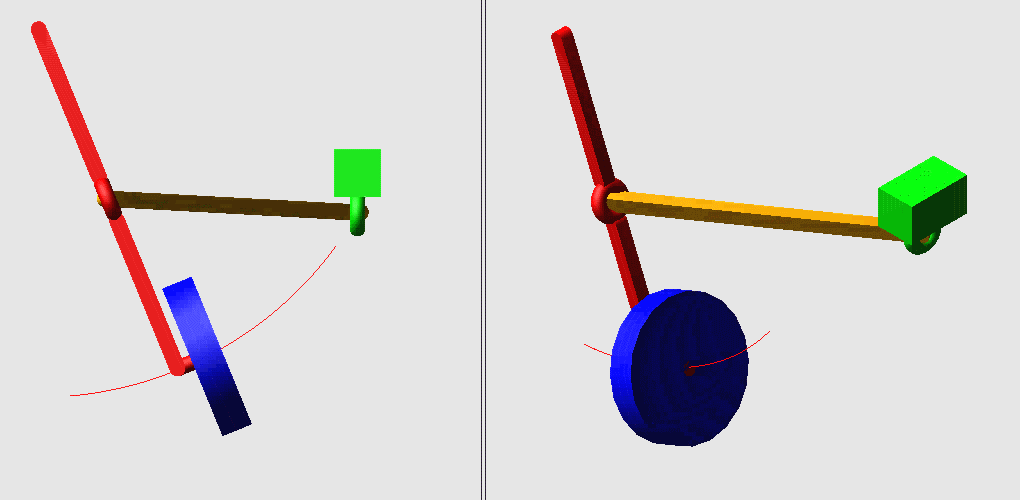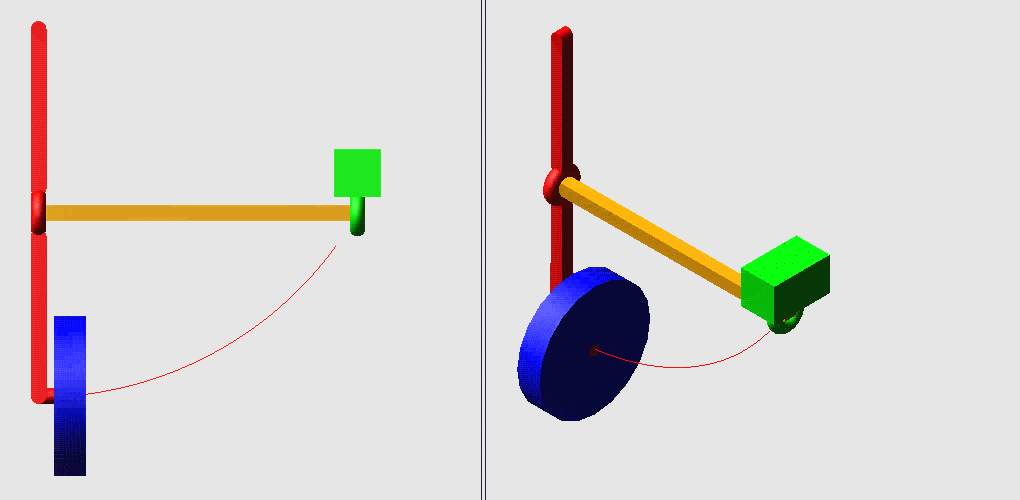
: z. O* ^3 L6 [% _: [4 m1.飞机起落架的收放机构
6 b2 }, Y! b. u, p. Q Q$ iN=4,g=4,Σfi=8,F=6(N-g-1)+Σfi=2! p" ^- b! D& M$ L1 S5 F- j& J
但是中间的杆两端分别构成球副,可绕自身轴线转动,而这个自由度对整个机构的运动没有影响,为局部自由度。& z& E/ B& i% H/ z3 X
1
 $ z0 g3 x6 d$ H
$ z0 g3 x6 d$ H
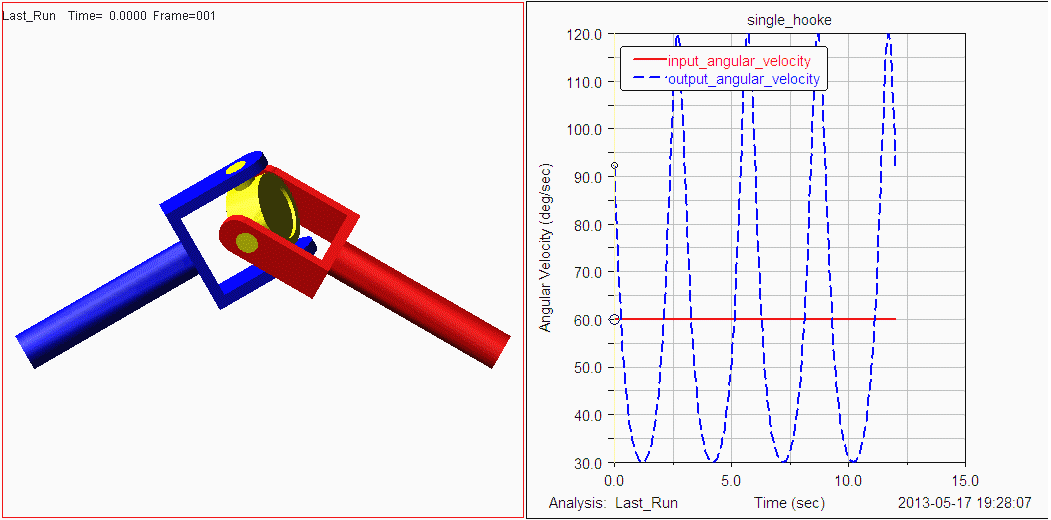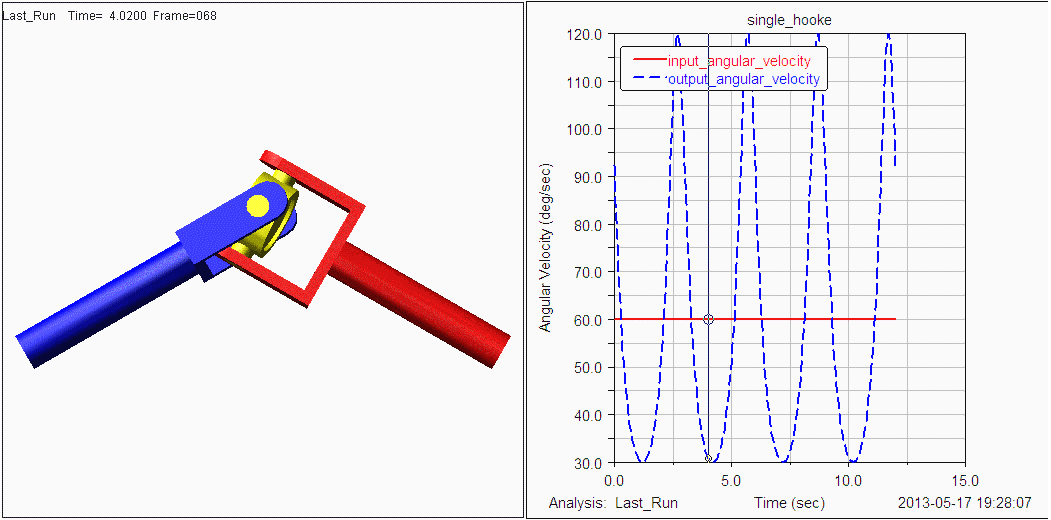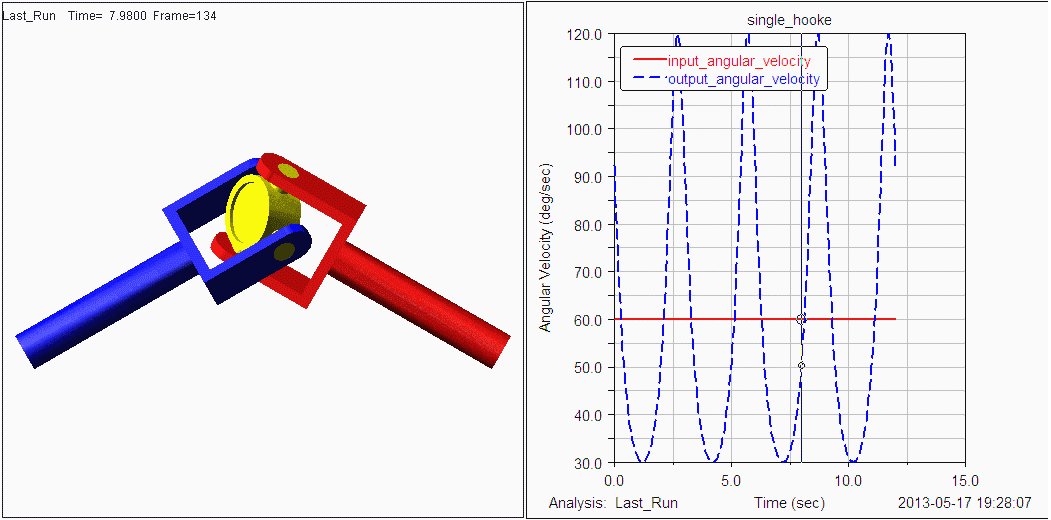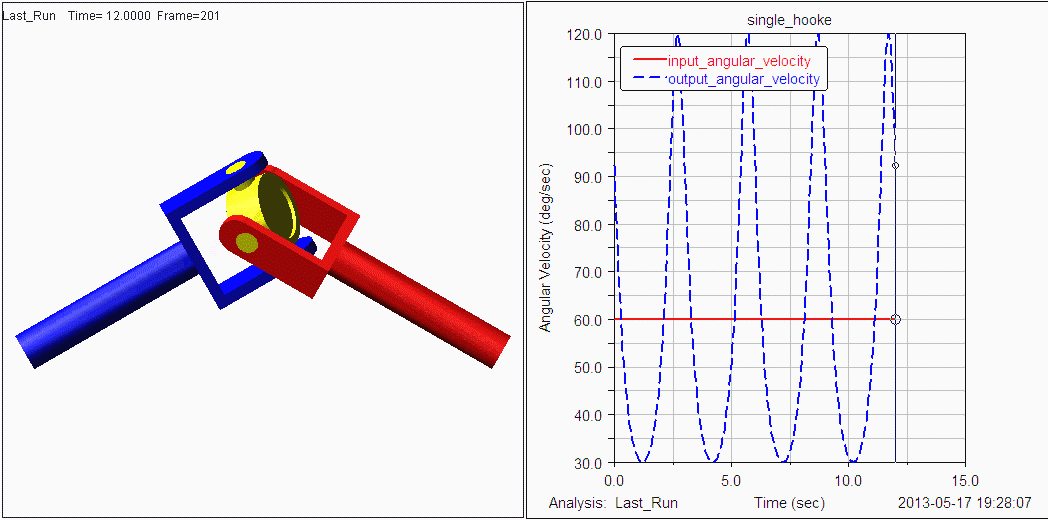
2.万向联轴器(虎克铰)3 Q3 G0 o- {* v$ @/ q8 e- h H" I0 S5 T
N=4,g=4,Σfi=4,F=6(N-g-1)+Σfi=-2+ B/ ]: q; ]5 L; ^: ?5 o! W# k
显然与实际不符,只需一个主动件的输入运动。
% } `% Z, _. s; X' i0 y# w4 F
2
 ) b9 h' a ^- Q8 w/ x1 N2 y) t8 P
) b9 h' a ^- Q8 w/ x1 N2 y) t8 P
解释——G-K公式本质:$ K: p7 d* f5 R
体现机构构件和运动副之间的关系
# J; `( {8 K5 r2 s$ [8 F$ J6 t违反这一公式,必有运动副没有完全发挥其约束功能。具体包括:8 A# G9 ^% @9 i$ J. H# f+ Q
1)由于特殊几何设计及装配条件,这个运动副在实际运动中并没有完全实现所有可能的相对运动,即产生了局部自由度。
" G; N9 |7 I& r6 v, A! g( z+ r如1.飞机起落架的收放机构。
6 k6 |1 F K, n) q1 S: e2)机构中冗余约束及公共约束的存在。
: w% @6 |# q% |0 g如2.万向联轴器(虎克铰)
" h7 T5 i% r& V) s+ Z# P1 `) V0 h
对G-K公式的修正
$ N/ q5 i* O" j; C, b6 L# u& U6 b% A
F=d(N-g-1)+Σfi+ν-ζ. S3 {2 v3 }* c' D: U
d:机构的阶数,由机构的公共约束决定,不是传统公式中的3或6
( F, Q- U" y7 _$ B/ F/ rν:机构的冗余约束数* N; V Q$ U5 ]: D& P
ζ:机构的局部自由度数3 h$ X8 N# @* n, I
+ m. S$ {% {. t- a1 [重算1、2的机构自由度:0 N x. ^2 o" A5 o7 Q% J
1.N=4,g=4,Σfi=8,d=6,ν=0,ζ=1,F=d(N-g-1)+Σfi+ν-ζ=1: `" f) w# U; y9 A8 w
2.N=4,g=4,Σfi=4,d=3,ν=0,ζ=0,F=d(N-g-1)+Σfi+ν-ζ=1% f! T/ _5 D* Q6 r$ g
符合实际。7 b1 j i" i, g, S0 t& D) `7 {
1 d2 p1 r& q% q5 C9 P |