【20160218】机械原理|常用机构
6 u2 q! z) }/ K7 h0 d
6 k$ S8 m3 q5 t6 i x9 C7 J同源机构, |; j, j4 q( K S( @
- f$ l* o8 Y% J$ e& S
四杆机构中有一个非常有意思的现象：3个四杆机构可生成同一连杆曲线。这就是有名的Robert-Chebychev定理。 + k* y# Z8 m0 P" a
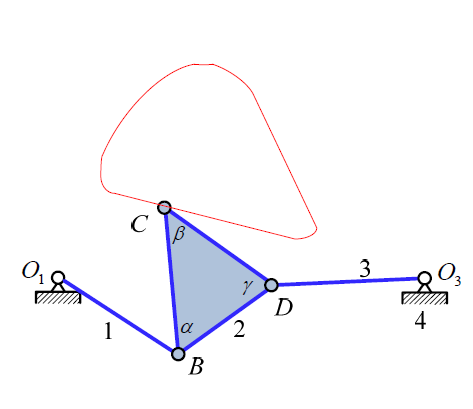
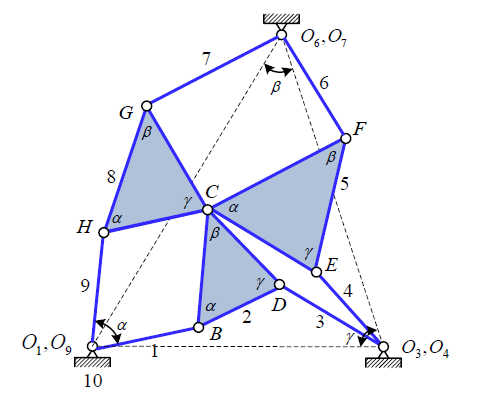
首 先 考 察 一 个 如 图 1 所 示 的 铰 链 四 杆 机 构 ， 选 择 点 C 作 为 连 杆 上 的 参 考 点 。 通 过 几 何 方 法 ， 可 以 得 到 图 2 所 示 的 另 外 两 个 铰 链 四 杆 机 构 O9HGO7 和 O4EFO6 。 这 三 个 机 构 在 点 C 处 具 有 相 同 的 连 杆 曲 线 。 5 W! g$ l2 e1 I7 L0 ~
1
2
# W! T' C9 R* B4 O' t/ r
几 何 条 件 ： （1）O1 与 O9 重 合 , O3 与 O4 重 合 ; （2） O9HCB 、O3DCE 和 O6FCG 都 是 平 行 四 边 形 ； （3） ΔBCD 、 ΔHGC 、 ΔCFE 和 ΔO1O6O3 都 相 似 。 i1 I1 E* y8 U+ K
规 律（正 确 性 待 验 ?）：杆、三 角 形 一 边 平 移 为 三 角 形 一 边 、 杆 ； 相 似 得 机 架 点 位 置 ； 三 角 形 相 似 得 另 两 边 ； 连 接 。
! E F( |0 Q: V" F* a1 E6 b L
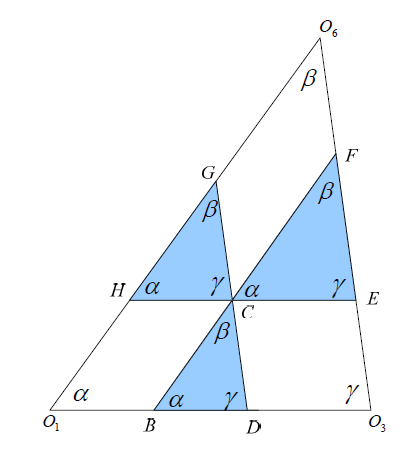
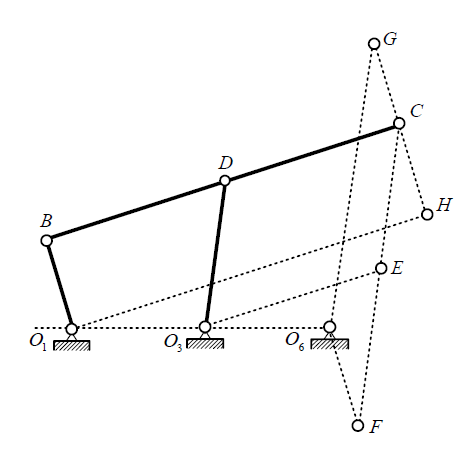
8 O) n' k8 ^2 I7 O; c( T0 Q3 ^还 可 以 通 过 "Cayley 图 谱 ” 方 法 得 到 同 源 机 构 的 结 构 参 数 。 具 体 如 图 3 所 示 ， 假 定 3 个 机 架 点 的 位 置 未 被 锁 住 （ 可 移 动 ） ， 将 每 个 机 构 拉 向 各 自 对 应 的 机 架 ， 直 到 退 化 成 一 条 直 线 。 这 时 ， 所 有 移 动 构 件 的 长 度 不 变 ， 所 有 的 角 度 也 不 发 生 改 变 ， 唯 一 变 化 的 是 3 个 机 架 点 的 位 置 ， 即 机 架 的 长 度 发 生 了 变 化 。 利 用 这 种 方 法 ， 可 以 得 到 任 意 一 个 四 杆 机 构 对 应 的 另 外 两 个 同 源 机 构 的 尺 寸 。 例 如 ， 通 过 该 图 谱 可 以 得 到 图 4 所 示 机 构 的 同 源 机 构 。 元 机 构 的 连 杆 参 考 点 与 连 杆 的 两 个 铰 链 点 在 一 条 直 线 上 。 ( 就 是 那 四 个 平 行 四 边 形 拼 起 来 了 ~ )+ b' A8 X* F6 h. Q+ G! a
3
4
8 V8 E9 E- o: h' ~
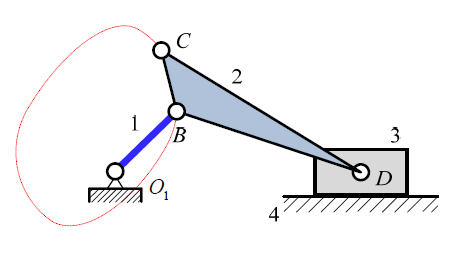
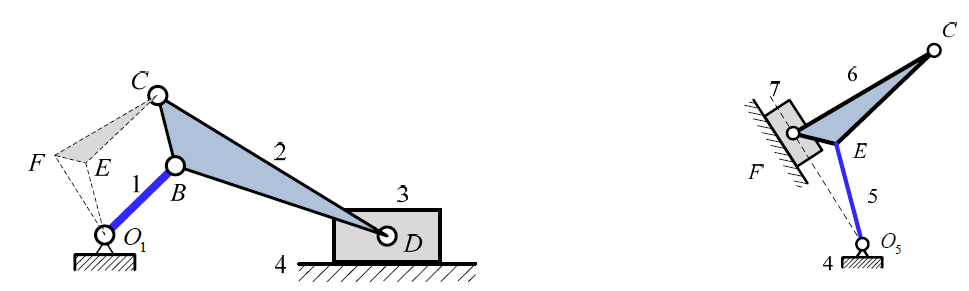
曲 柄 滑 块 机 构 也 有 同 源 机 构 。其 中 O1ECB 为 平 行 四 边 形，ΔBCD 和 ΔFCE 相 似 。' E, ?, I: o. k, d$ y# `
5
6
j* {7 ?. }% L, H+ _ w5 H
规 律 (？)： 杆、三 角 形 一 边 平 移 为 三 角 形 一 边 、 杆； 机 架 另 一 端 类 型 保 持 一 致 ( 滑 块 ) 。3 S5 e, D3 t3 Y# G$ D' R
: F9 S, F9 y0 D5 k' X/ | |
楼主: 黑森林的鹿
发表于 2016-2-16 10:46:33
并不是什么高材生啦