本帖最后由 动静之机 于 2013-6-28 19:19 编辑 1 n& @% W1 u1 R* F6 i4 J% @
1 E; b: K; U/ D* K$ K' D
3 q( u& h! l- i& y. o
' B: L* ^* j" r0 z) F
- }% g! f+ \$ \6 {3 P: d3 G
( p7 J( A% C4 Q" l- ]. ^" f; I
3 e/ p4 e+ |5 ^: y! H! b# |% F- T
目前网上查不到国产的此类车床，于是估计本帖是首发了。
8 J, d/ a' b3 y, o6 V7 m2 o也许此贴过后，很快就有山寨，拭目以待。
, A% O i/ x6 h6 m- H% P ( W6 C/ h! }) m. A0 c/ v
正如这个帖子过后，国产的相关工具很快就有了，足以证明社区巨大的影响力： rotary broaching 旋转拉（推）削原理------内四方、内六方等问题的答案
1 s. X5 O1 }( A7 W) Y" Vhttp://bbs.cmiw.cn/forum.php?mod=viewthread&tid=143588
9 I Z5 }/ l2 c
) @$ I9 t+ o9 u7 H( \* |) R% A8 e q% W& ~2 z2 x
www.vicmarc.com 官方资料：
VOD Aug 10.pdf
(1.59 MB, 下载次数: 26)
2 G) N9 k5 j! {; L- E \9 ^% w
- f; Q/ Y# F3 g, G0 T" y" b
先看看常见的方法：工件定心回转: F' F/ N7 u C4 r; \ F4 a
方法一： 刀具做径向跟踪，即径向往复直线运动的频率是工件旋转运动频率的两倍，同时轴向走刀，以形成椭圆柱。 例如发动机活塞椭圆裙部的车削。好在径向尺寸变化量很小，不然很难实现高效车削。 4 H7 N' h3 O: N: |
! K) Q8 G7 f: m8 Y6 N- H
9 V6 s1 b' ?8 Y, J5 @! C
方法二：刀具径向无需追踪，仅轴向走刀。该方法利用圆柱的斜切面为椭圆这个现象，将工件倾斜地夹持在主轴上。虽然没有理论误差，但加工完毕后的零件边缘和零件平面不垂直。这个方法勉强可以对付平板的椭圆圆周，对腔体（椭圆碗）就无能为力了。这种方法加工的椭圆，短半轴长度为圆柱半径r，长半轴长度为r/Sinα
1 r& \0 b' x5 O! x4 ?
' |& ^1 ]- j' D 然后是特殊的方法：工件偏心回转
0 X9 I+ _5 Y ?$ k( N! { 方法一： 凸轮仿形 ----应该淘汰了。 16世纪欧洲人用这个方法
1 d6 Q. V* a) ^来加工象牙，转速不能太快。
0 T* `& |/ h, Z$ `& Q
& k' X. q% s; B2 W* f2 {方法二：使用十字滑架工装 ------- 无理论误差 ---- 初级水平
: q3 P/ V* C2 s! `7 Q. d( T
6 n% N" k: y9 o% H! H
这货和椭圆规长得一样是吧？
# [, Z0 k8 G; q7 P5 Q
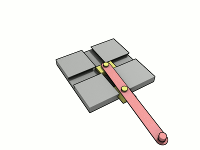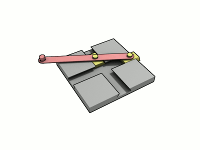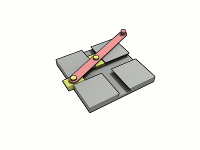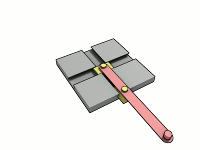
的确如此，相对运动： 滑架不动，摆杆走椭圆；摆杆不动，滑架走椭圆。 至于滑架的具体结构，每个设计者有自己的办法，见前面的附件。
+ g& O) T' }: I2 @0 a& c" M9 A; |2 t) H9 C8 y# W; Z, y# }
方法三：使用两个旋转运动合成 ------- 无理论误差 ----- 最初设计这个的的确是高手
& a, Y0 x8 G6 q8 D- m 第一眼感觉，晕~~~2 \. i. L7 L. r9 Q- A
5 u# `: L+ d s( x1 a
原理铺垫：半径为R的小圆在半径2R的大圆内滚动，除了圆心和边缘，任意点的轨迹都为椭圆。
& L% j' [$ Y D9 r证明： 小圆在大圆最右侧停住时，切点位于X轴上。在小圆圆心的右侧距离r处取一点，此时α=0。 小圆逆时针滚动（红色虚线为圆心轨迹），方位角抵达α处时，在大圆中转过的相对角度是2α（顺时针）。 因此该点落在XY直角坐标系中的坐标是： X=R* Cosα+r*Cos(α-2α)=(R+r)*Cosα ----① Y= R* Sinα+ r*Sin(α-2α)=(R-r)*Sinα ----② 即：
: |( ]" c5 m' j
---- ③
% o. ]$ v/ S! j) y' ^4 c( u这便是个典型的椭圆方程了。& l0 Y6 U- f( X; G* q- D
这个证明意味着：椭圆可以由两个旋转运动来合成，不妨称为自转与公转。考虑到偏心的震动随着半径的增大而增大，因而把回转半径比较小的那个转动作为公转偏心处理。 图中，可以清晰地看见，车削外圆时，前后角不断发生变化，刀具的前刀面选择不好的话，会出现负前角的情况。
8 y% L" _2 `6 j( ]
: @& X. _ V" Q, P+ Z2 G" q( N. P
就算偏心再小，高速回转的震动仍不可避免，于是人们设计了平衡块。平衡块位于工件质心对称位置处，配重 *配重偏心距离 =工件重量 *夹具偏心距离， 当然夹具本身先得做好动平衡。
9 N9 N; p0 }# l5 Y' w
; U, t+ U2 `# N& w" S* M
普通车床车削过程中，若车刀的高度不在工件水平线上，仍然可以车出圆形，虽然大小有差异。
2 @* k8 F; Y4 U7 U而车椭圆的刀具中心高度位置不能改变，不然轨迹就会发生偏斜（有相位差）：
! S1 u* {$ z8 m, K
4 [( ?; m, T& l' H& Y
所以这种车床配备了光学投影引导线，便于人们使用。
6 |5 k0 X8 g& Y/ k+ C好在车削端面的时候，角度是恒定的，所以车个木头椭圆碗，还是没有问题的。
9 M9 {) p% f5 M. }6 j准备试制的朋友，注意安全！！！ & w" M) S& N3 [
! Y O. j6 u$ f8 c: q* \ 延伸一下： 继续看上面的证明步骤，如果 r=R，即选小圆上和大圆相切的点作图，则②式变为： Y=0 意味着该点轨迹成了一条过起点和原点的水平线段（下图红色线段），长度为大圆直径。请注意，黄色箭头的反向延长线和小圆的交点刚好也是小圆与 Y轴的交点，即小圆直径上的两个端点分别始终在 X和 Y轴上滑动。同时，式子③中的 R和 r的数值在数学上无所谓大小之别，也就是说在小圆的外侧取点也无妨。这。。。。。。。。不就是椭圆规么？ - w; M/ a- ~8 V8 U- h3 W5 Z
继续延伸一下： 上面是让把两个旋转运动都交给工件主轴去做了，所以刀具仅需要做线性移动即可完成尺寸（不然怎么好意思称为车床呢）。如果只让主轴做一种运动，那么刀就得转起来，而且这两个轴有一定的平行距离（就是那个偏心），转速还得有比例关系。
+ t5 K" O% P# D. s1 o N) e8 |+ |) l一把刀能切出一个椭圆，两把对称分布的刀切出两个正交椭圆，三把均布的刀切出三个120度分布的椭圆。 T8 h8 V! e0 D2 h3 E& x
这。。。。。。。。不就是多角机床么？
1 n1 ?1 X f. {# A. Z6 k% M$ U8 E
显然这些面是有点凸的，但通过合理选择回转半径，可以获得近似平直的效果（越扁越好）。这个方法的好处是，由于刀具和工件皆做定心连续回转运动，无需停顿，因而转速可以比较高，效率自然也高。
" F" o5 R5 F2 O* s4 ]当然，椭圆的画法还有很多，但不是每种画法都能变成好的加工方法:
1 c! A: x6 I1 [; t1 ]6 C
8 D2 s3 d: V, Y: ?至此，这个奇妙的椭圆车床原理就已经说完了。
) `, }4 @; H+ y4 `以上讨论的椭圆是“普通”椭圆，或多或少还能用纯机械的方法搞定。 - c' [8 X# q5 \7 {4 j
这里还有一种另类的椭圆，即二阶椭圆，多用在流量计上：
6 U7 b2 J$ C, I* ?
当年的工程师，用描点 +放样搞好凸轮，做了两台滚齿机。如今，只要您的机器够快（运算），就可以滚的（仅限凸节圆）：
, G d2 r7 H! |4 {3 v0 d( \ v# p- r! h& Z3 A
/ Q" R- F9 f- I' z
这里有赏心悦目的高阶的曲线转动形式（南京加加的高手做的）：
/ C* D7 N2 r: u
! Q* f* t6 |7 K2 A6 ?0 c6 B' m9 q | 
发表于 2013-6-28 18:58:09
