|
方法二,这里提到了SVD算法 ) y" W3 C ?0 L0 }9 q5 N
通过实际的坐标点例子,来直观解释通过SVD求对应的坐标系关系。 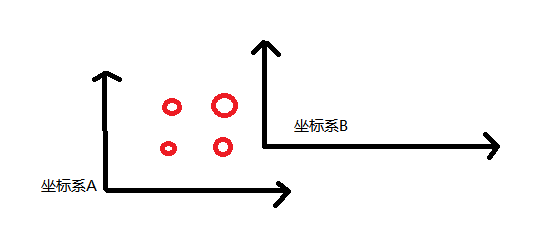 已知四个点在坐标系A中的坐标为: (0, 0, 0); (1,0,0); (1,1,0); (0,1,0) 可得矩阵A为
" S& v; `) v, ~% |6 [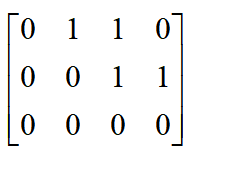
7 u; k( T6 l! a; A- n矩阵A这四个点在坐标系B中的坐标为: (2,2, 2); (3,2,2); (3,3,2); (2,3,2) 可得矩阵B为 ) d' m6 U- A! L9 M" [
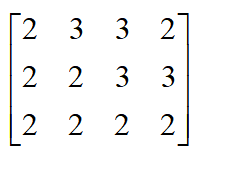
! E- \( Z w9 C$ X矩阵B步骤一:求两个数据集的质心 根据上述公式,可得质心为 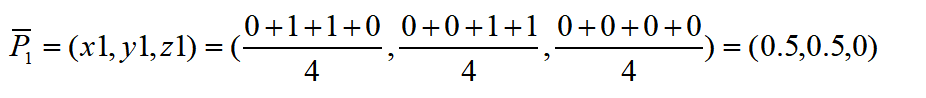  步骤二:将两个数据集的质心移动至同一个点,即只存在于一个旋转的转换关系。 对应坐标系中的点同时减去质心,计算后的矩阵A和B分别为 8 e* y2 ?0 t8 G1 Q7 S
 ! j9 u& {4 R. b9 T1 h; p ! j9 u& {4 R. b9 T1 h; p
计算后的矩阵A2 ?$ w4 | P7 a# C
 6 N3 u5 f/ u8 d 6 N3 u5 f/ u8 d
计算后的矩阵B备注:此处的矩阵A和矩阵B一样,因为举得例子较为特殊,只存在平移关系。计算过程通用。 步骤三:通过SVD算法计算旋转和平移关系。 定义一个3X3的矩阵,将矩阵A的每一行数据与矩阵B进行点乘,会产生四组3X3的矩阵,将这四组数据求和,得到最终的3X3的矩阵,就是我们需要用SVD算法来进行奇异值分解的矩阵H。 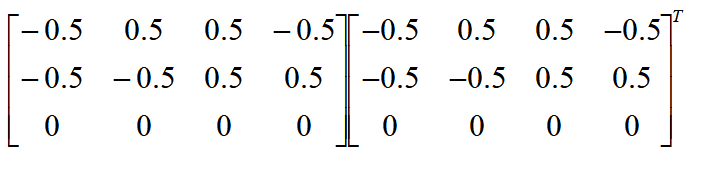 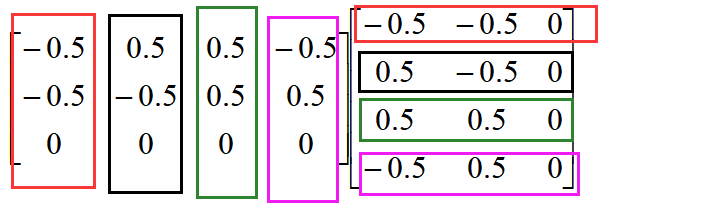 上述公式中,颜色相同的框内数据进行点乘,构成3X3的矩阵a1,a2,a3,a4。 矩阵H = a1 + a2 + a3 + a4。计算结果如下 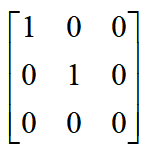 通过SVD算法分解该矩阵,这里直接通过MATLAB接口调用,具体原理在前面的章节中已描述。 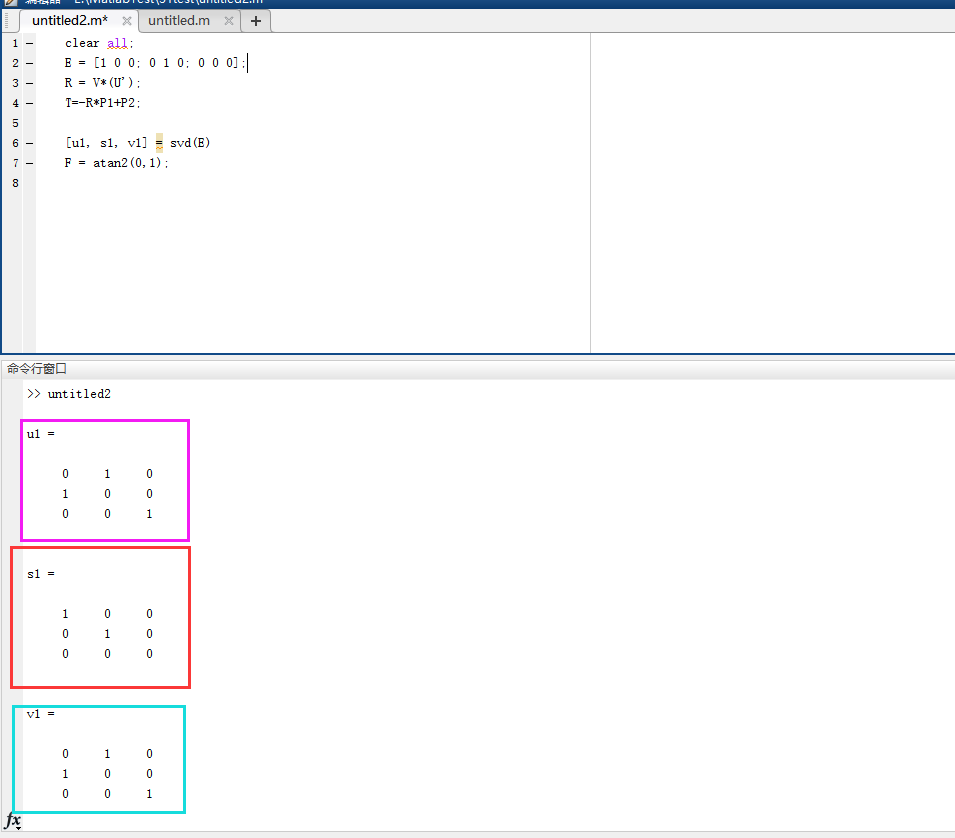 步骤四:计算旋转和平移关系 根据上述求出的u1和v1,可求得旋转矩阵R为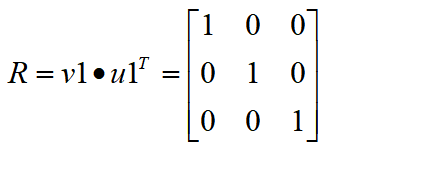 将该旋转矩阵转为欧拉角则Rx = 0, Ry = 0, Rz = 0。 将该旋转矩阵转为欧拉角则Rx = 0, Ry = 0, Rz = 0。根据公式 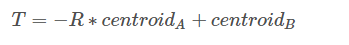 得平移矩阵为 得平移矩阵为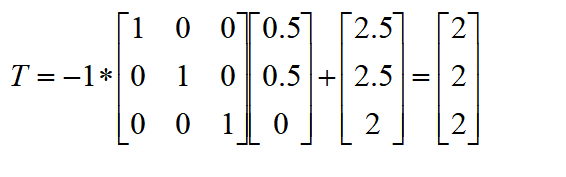 总结:如果在实际项目中,需要获取多台设备间的关系,如机器人相对于产品间的关系,或者机床相对于产品的关系,则该方法较为实用。注意:在实际的选择参考点时,不要在一条线上选点。如上述选的四个点,要求不能共线。要不然会减少有效数据。 u4 I" S1 x0 o" T7 _8 y
|