传统道碴路堤温度场分析

元计算

1.        问题描述

图1为传统道碴路堤模型示意图。忽略风的作用，考虑气候变暖对传统道碴路堤长期热稳定性的影响。以下对其修筑完成后第2年和第50年的温度场进行分析。考虑对称性，取一半为研究对象。

图1 传统道碴路堤模型示意图

2.        区域内控制方程
+ n4 s! V" o- l% ^/ C! ?+ x) S

在计算中对于含水介质中相变潜热问题采用显热容法进行处理，假设模型中含水介质相变发生在温度区间(Tm±ΔT)。当建立等效体积热容时，应考虑温度间隔ΔT的影响， 同时假设介质在已冻、未冻时的体积热容Cf和Cu及导热系数λf 和λu不取决于温度，因此简化构造出Ce*和λe*的表达式如下：

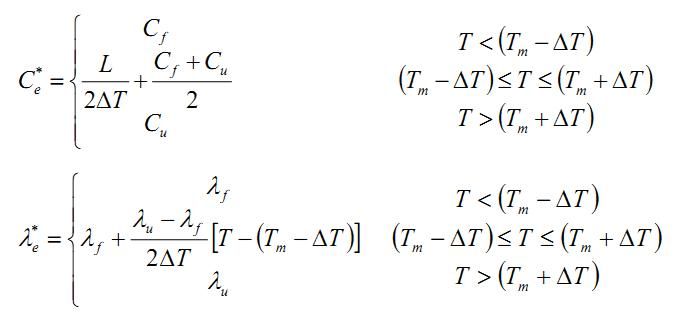
式中：L为含水介质单位体积相变潜热。

3.        材料参数

各介质材料参数见表1。

表1 路堤结构中各介质的物理参数

4.        边界条件与初值条件

4.1. 给定温度

考虑全球气候变暖的影响，取青藏高原未来 50年年平均气温上升 2.6 ℃，设初始年平均气温为-4.0 ℃，对各计算模型的热边界条件进行如下设定：

天然地表 AB和 IJ的温度按下式变化：
6 z0 @1 v( E! |3 ]( t

路堤斜坡 BCDE和FGHI 的温度按如下规律变化：

路堤顶面 EF的温度变化规律为：
  o' M- W. L# n; O4 H

式中：th为时间变量，当α0=0时，th=0对应的初始时间为7月15日

4.2. 给定热流密度：

4.3. 初值条件
2 J' K7 h. V/ A$ f+ x

5.        时间步设定：

	起始时间	终止时间	时间步长
定义计算数据/s	0	63072000	432000
对应实际时间	第1年7月15日	第3年7月15日	5天

试算两年，共146步；

第2年 7月15日对应为第73步；

第2年10月15日对应为第91步；

6.        网格剖分

四节点四边形、三节点三角形

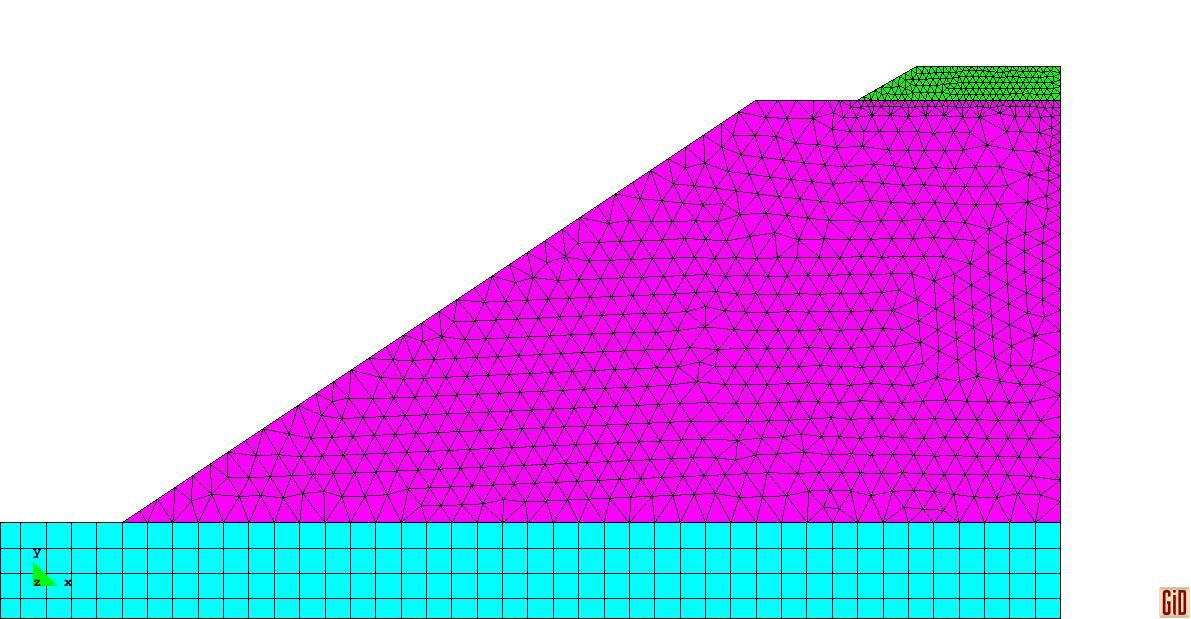
7.        结果

第2年10月15日温度分布云图
6 C8 K5 C, N8 p3 {; U2 e* T* Y

等值线图

赏花的盲人

好像很牛呢，值得学习。。

puntin

写几个有限元公式忽悠人呢