|
|
本帖最后由 动静之机 于 2012-6-5 13:46 编辑 - _; l# F+ O; r
; O1 P6 g1 e' E2 K( {4 g: y
参与过这几个帖子后感受颇多:" s% Y8 U7 G4 h9 D0 ~/ u w
: g* w) H6 o9 ?# o4 frotary broaching 旋转拉(推)削原理------内四方、内六方等问题的答案& x5 ~) Z8 m( ]% N4 W1 ~( d; C1 X
http://bbs.cmiw.cn/viewthread.php?tid=143588 9 v& `$ a- ~0 A/ `
- m$ B6 p# Y; E! q( Q' T
在不锈钢板上开等边三角形的孔,有什么方法效率最高?求助1 k: Y0 M/ d7 F3 ?9 @4 m6 u7 f
http://bbs.cmiw.cn/viewthread.php?tid=137359&extra=page%3D59 e8 t4 M! D- S" ]+ F7 l5 y4 J5 ], g
# x$ N, R6 w) h; r5 R5 R: F
谁见过可以钻六边形的钻头呀
, L% u$ B4 r2 d4 Shttp://bbs.cmiw.cn/viewthread.php?tid=144202&page=1#pid860848pid860848
% j' @% C8 F1 E: f
' P) i! }* Y9 v: K) A4 `后续查阅了一些资料,在此与大家分享一些相关知识。1 ?# `- t/ @! H- o
! W5 l, Z8 @7 n8 h- i' w1 z
先温习一下关于摆线有关名词:8 A7 |/ M3 g o- C9 M" x+ |
当一个圆在一直线上纯滚动时,圆周上的点所描绘的旋轮线称为摆线cycloid。- V- G: w" V$ x e. H% @
圆内部的点所描绘的旋轮线称为短摆线curtate cycloid。
! d. g2 q* F3 @: W$ Q圆外部的点所描绘的旋轮线称为长摆线prolate cycloid。
) j3 ?+ ]( G3 T短摆线与长摆线合称为次摆线trochoid。
: s1 }2 M; b& z7 b
1 ]9 U; q l b6 J6 s; {/ Y* q9 [, p+ v. C, g
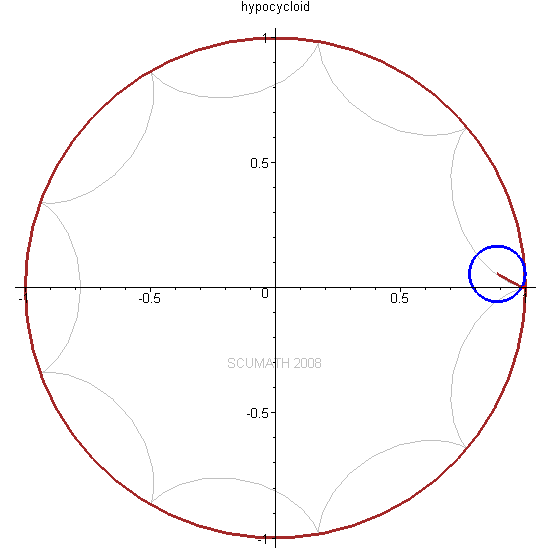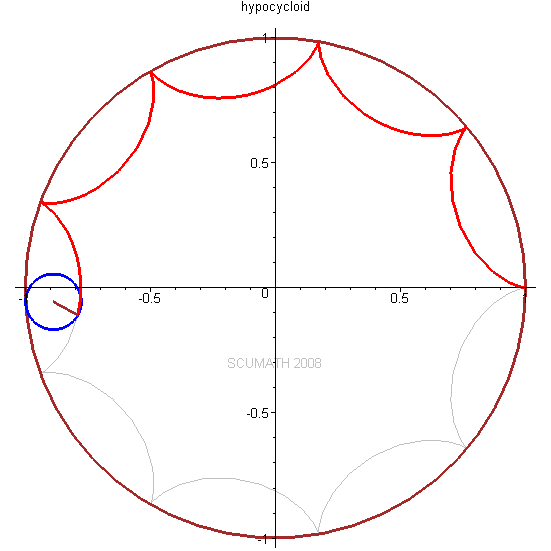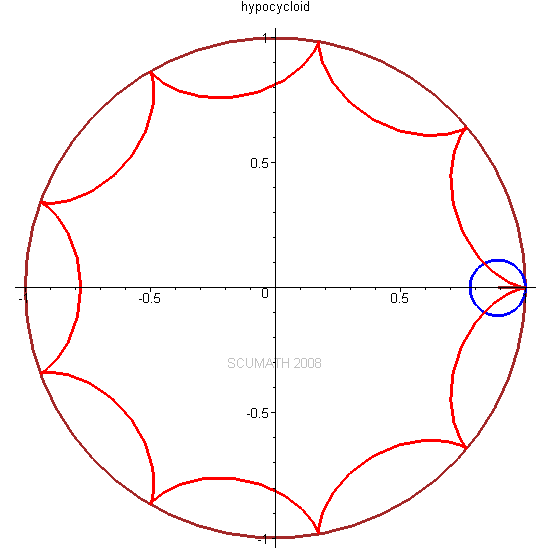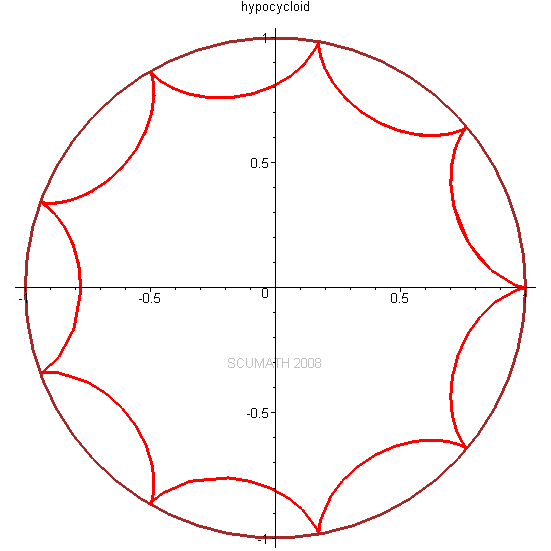
当一个小圆在一个大圆的内部纯滚动时,小圆圆周上的点所描绘的# f/ @* L7 @' l+ l5 R s: |* D' X7 D8 J
旋轮线称为内摆线hypocycloid。
8 S# i K, M1 b6 @6 ~4 ?+ U小圆内部的点所描绘的旋轮线称为短幅内摆线curtate hypocycloid。4 _0 J, }9 u# z4 c5 I
小圆外部的点所描绘的旋轮线称为长幅内摆线prolate hypocycloid。7 |# q2 k; F7 g) A9 m5 k: p4 I
二者合称为次内摆线hypotrochoid。3 A# {7 k1 Y& f$ w* O, L
9 z6 d6 z4 Y: \% p, t

' a7 v' e0 t/ @. j- h 8 |( a, c# n3 z$ G" v0 [/ w/ F& N
/ Q$ L$ s3 @8 J- y
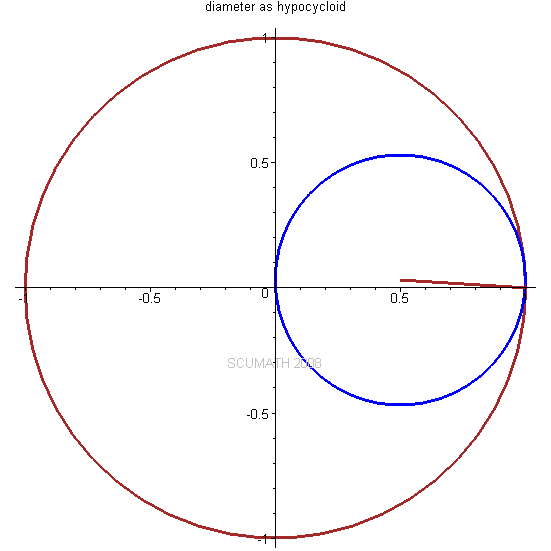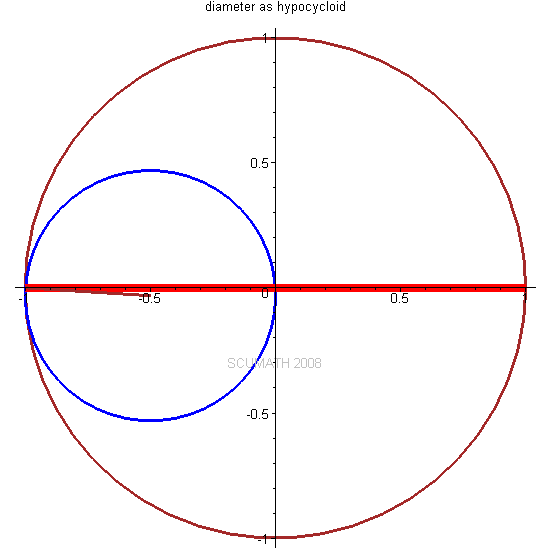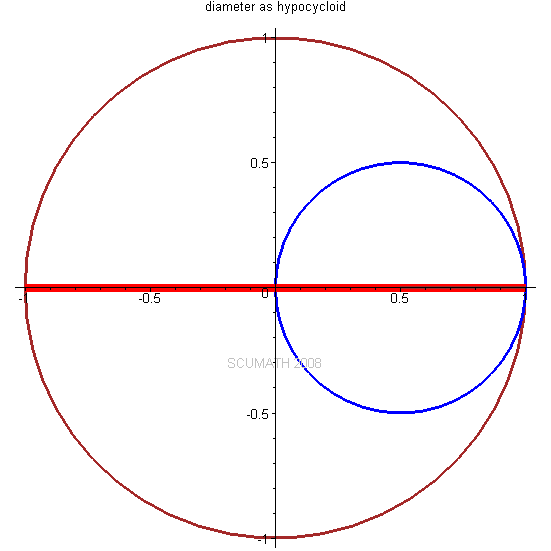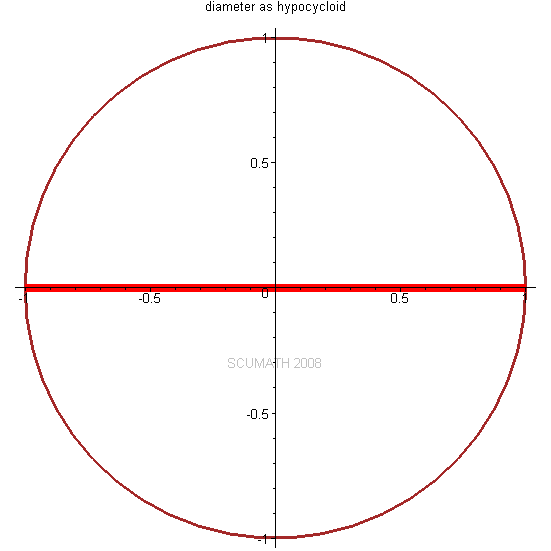
* p# k& q- E; C6 b7 O
2 C2 Q, K' A6 ?: ?$ Z$ }
 ) I% w" w; G7 k1 `/ J* ~% C9 H
) I% w" w; G7 k1 `/ J* ~% C9 H
: t" N$ n3 L3 a% K8 S
$ Q6 M P* ^/ }2 V4 O, l: ] 8 O J5 g- y* a' r3 F
当一个小圆在一个大圆的外部纯滚动时,小圆圆周上的点
2 x8 D: @' `: F$ }* V4 K* _; P所描绘的旋轮线称为外摆线epicycloid。, x" s& R0 s- ]* e/ w$ P, s! X
小圆内部的点所描绘的旋轮线称为短幅外摆线curtate epitrochoid。
; V0 X+ h Q v& w小圆外部的点所描绘的旋轮线称为长幅外摆线prolate epitrochoid。# R0 K1 N6 I' f! S/ b
二者合称为次外摆线epitrochoid。
# P, f! O0 y2 D(图略)! X; y' @; C8 U: V
( @- r2 `( @$ Z) F虽然这些名词不难理解,然而接下来的应用却让人大开眼界。$ v6 V9 N& L* v! {
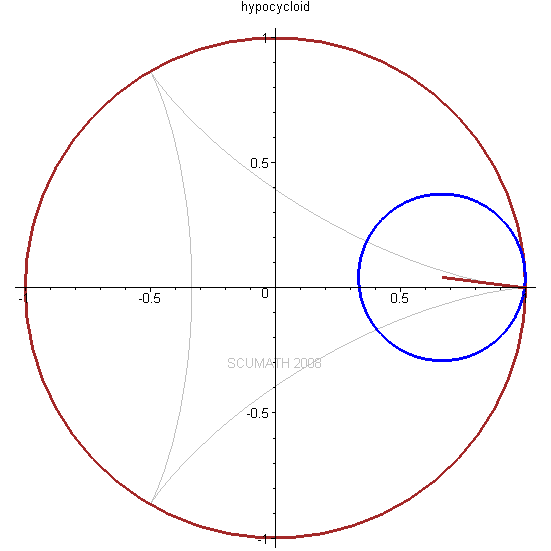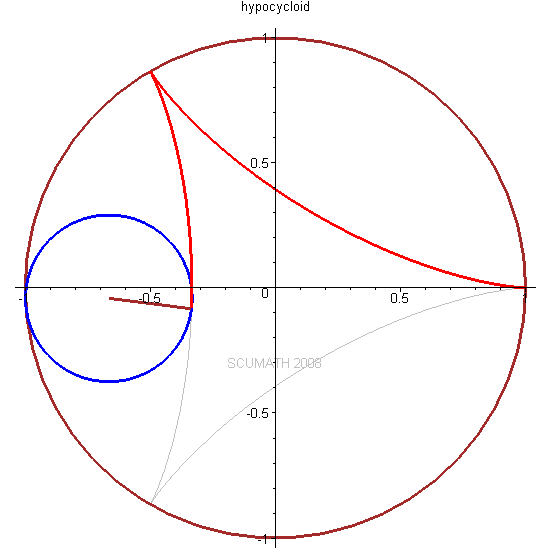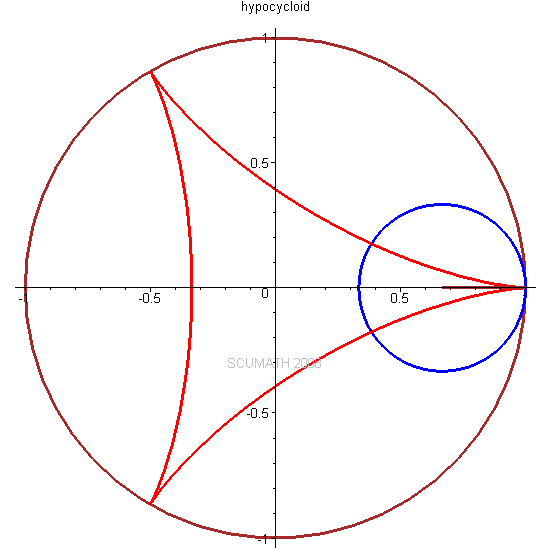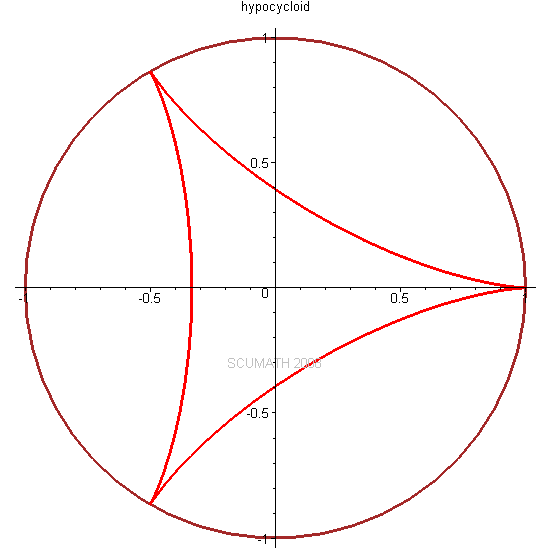
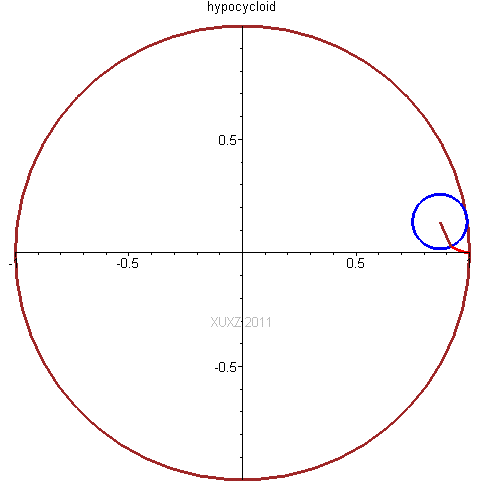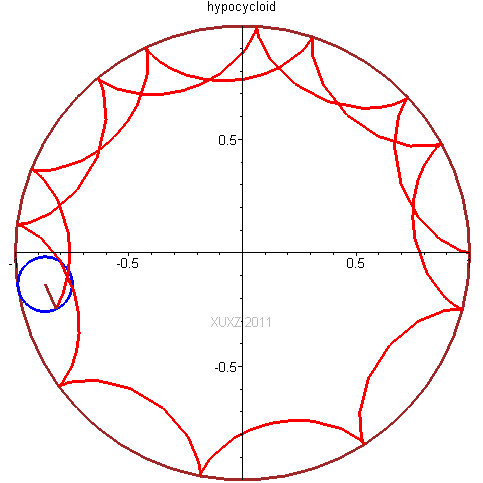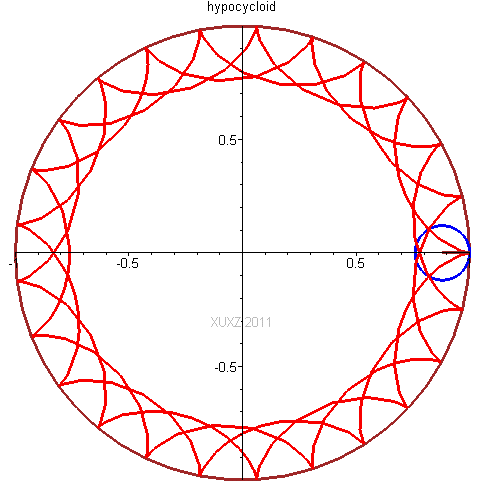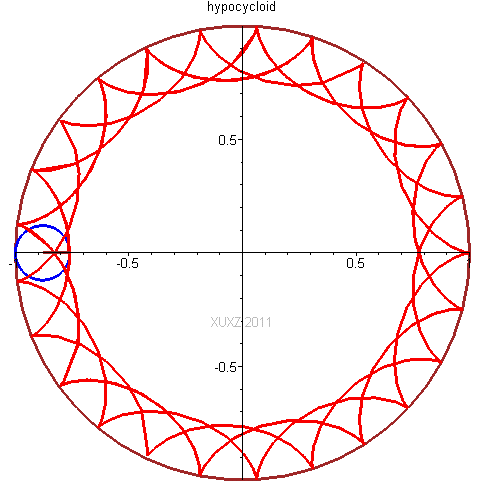
! @2 |7 Z6 x9 T+ n! {9 H1 Z以三叶状次内摆线为例,不同点扫描过的曲线都不一样。
" z; C h% F$ p ( c* C3 p; g4 N# g3 x# G% o ( c* C3 p; g4 N# g3 x# G% o
1 r$ ] _! e# M. @' j4 ?( a# t5 s
9 r- _) K. a. G( D/ Z当长臂为短臂长度的3.5倍左右时,可以得到比较理想的三角形:0 u$ A @+ L2 m5 b# w6 q4 b, C
 ( U. `0 b3 O) e ( U. `0 b3 O) e
- Y4 c. w/ Y. m2 T5 b
% l- D. ]. B1 y8 L然而如何巧妙地将这个自转与公转半径比、周期比、相位差用具体的机构
8 |; [3 p$ w2 h6 i实现,是个技巧问题。这里有个实例,供大家下载后研究。
( N5 h8 o" p2 z) V: [6 k8 g
 钻镗三角形孔的方法.pdf
(151.36 KB, 下载次数: 533)
钻镗三角形孔的方法.pdf
钻镗三角形孔的方法.pdf
(151.36 KB, 下载次数: 533)
钻镗三角形孔的方法.pdf
9 o! y( D/ g" ^& m0 e5 [' Z( A
1 [6 v9 s/ r" C' ]; g; `. g上述三角孔钻床实现的方法是:把一个正常的旋转的主轴以二倍的转速(对地)反向" I+ J* i, x3 N. ?1 i+ J4 P" {
公转,把偏心率控制在需要的值。使用的刀具是扁钻。
% a5 c3 L: S' X2 d. t* s L" u0 z" F0 s# W
它的数学原理是:既然这些曲线任意一点为两个旋转运动(矢量)的叠加,那' E9 Y3 S" b3 Z, U' Z
么具体是矢量A+矢量B 还是 矢量B+矢量A是没有区别的,因而就可以转化成:7 i D' Z/ E- I; R' U
 9 u6 K( k0 _; b' n2 t3 B4 J# } 9 u6 K( k0 _; b' n2 t3 B4 J# }
) M2 f3 C$ v3 F1 @3 u- d: v) }
" O+ w% i4 p, C9 ^请注意,动画中蓝色箭头总有两个位置互为180度的位置而红色(偏心量)位置相同,
H' s3 O( ?3 O* J6 g9 m- x1 l I- m即意味着加工三角孔时可以采用两刃刀具(扁钻)。
9 T5 f. W1 e0 b% D( e
4 z: e; k) y6 y/ C: n+ P. d" D6 ?( W/ l4 Y3 |4 }4 q& N; q5 ^5 J
 , F, S; D8 j/ E( n( s5 X" Q , F, S; D8 j/ E( n( s5 X" Q
" x9 v* g% ~7 d! u. C
这极有可能正是麻花钻(两刃成180度相位)打浅孔或薄板经常成为三角形! M0 A5 R: C4 }' H
的本质原因。由于钻杆的柔性或者手持的不稳定性,钻头本身在自转的同时
9 U, h7 }( k* z# @9 G有抖动现象,只要稍有走偏(横刃等因素的综合影响、只要半圈就够了),, a8 w2 O) d! ~* T; E; V
这个误差就会引正反馈强化而最终形成三角形。
, R5 k& \& ~& P7 c7 z% }* l ?; I' t9 k! x8 j& x
同理,更多的边数也能搞定。也不难证明,用上述方法时,- G" o* J9 a9 Y( B( m2 q
加工四边形孔的刀具截面是三棱形,
2 [; B. ]" @& K8 N加工五边形孔的刀具截面是四棱形
- w( w' M& U. G& H$ w加工六边形孔的刀具截面是五棱形
. c! I) k) |/ Y& W* ^# K8 @; O0 n、、、
9 x" \3 d) Y! n# X; E \ * W9 q) N# }+ a+ ~/ w% N J( \& [( v * W9 q) N# }+ a+ ~/ w% N J( \& [( v
如果换个角度看问题,你会发现这个方法不但适用于内孔,同样适用于外表
7 a. `+ A( T/ k面。这就是很多人迷惑的问题:为何车床能加工多边形。这个技术玩的最好4 a4 s* h3 l. r0 E: @
的恐怕是德国维拉WERA公司(旋分技术)。
; \4 D) Y* t! V: ~5 a% ^5 y$ h# @6 N2 f9 o2 V. l
摆线的故事同样可以在双端面平面磨床(轴承、光学、芯片行业用)里找到。
: J) o# e- m# T, k1 {1 }' l# `, u) ]) }# N7 k+ v; {3 |% N% h
以上讨论了两级串联旋转机构的扫描轨迹应用,那么三级串联旋转机构呢?0 u g. V6 Z+ C
呵呵,以前讨论过的独臂时钟就是一例。秒针针尖的轨迹将会非常复杂。
$ i+ ^: o3 t5 ]0 C; }+ _% dhttp://bbs.cmiw.cn/viewthread.php?tid=124154
( k9 y0 C L( c; h+ R$ m+ z& z& o) k& M) m& e u

$ q6 E! N1 Z2 Q" g4 X3 @ y* P% }, E更多级串联旋转机构的轨迹?俺能力有限,无法继续推演,就此打住。$ d( G, b' `! y! V! n7 u
|
|
