1.NASA将直播波音Starliner太空飞船的关键测试
4 O% _* c- F) K @. {1 M0 h( I8 W8 a

4 C9 n5 D: {9 M& u" y
据外媒CNET报道,随着美国宇航局(NASA)进一步推动将近十年来首次载人航天发射带回美国本土,波音公司新的Starliner航天器的测试将意味着一次大考验。 1 c4 c) H+ q1 Y
目前,该Starliner航天器已经出现在新墨西哥州的白沙导弹试验场的测试台上,等待定于太平洋时间周一上午6点进行的逃生系统测试。该测试的目的是确保在发射台上的紧急情况下,四台中止发动机和控制推进器能够点火,从而将太空舱和宇航员带离潜在危险。 Starliner是美国宇航局(NASA)已签约的两架新型航天器之一,这是其商业载人航天计划的一部分,该航天器开始将宇航员飞往国际空间站。另一个是SpaceX 载人龙飞船 ; 这两艘飞船在开发和测试过程中都面临着延误,这促使美国宇航局局长吉姆·布里登斯廷公开向这些公司施加压力。
6 C7 |% U2 [2 i3 L" U6 ]+ o
2.清华将线性代数教材改为英文版,学生称更通俗易懂; h+ O, g8 `+ b( W- r1 G4 g- v
6 A8 p! _) k3 ^& x9 w

& O+ |* ^5 F( V" m' H( r( j( M
近日“清华大学将线性代数教材改为英文教材”话题引热议。刚刚参加完该课程期中考试的清华大学大一新生在接受媒体采访时表示,适应了这本教材的体系之后,从内容上来说,这本教材更通俗易懂,容易理解。 # E* `8 k) U* B, t+ ~
据介绍,教材的正式更换将于2019年新生入学,此前学校采用的都是中文版教材。对于语言问题,有学生接受采访时表示,刚开始用的时候肯定会有语言上的障碍,但是从语言上来讲,经常阅读教材,适应了它的体系之后,其实还可以。
0 C: i d0 M8 X0 K! L$ T ?
3.德国力推新能源汽车发展,2030年前将建100万个充电桩9 c: y. ]" k% F+ @0 D) Q0 Z
% e+ N! I8 D5 I# W% I

) E; \# `" V7 \# E
德国总理默克尔3日表示,德联邦政府将携手汽车业界推动出行方式的转型。为此,她即将在同汽车业界的对话中探讨新能源汽车购买补贴、充电设施建设和汽车业转型对就业的影响等议题。默克尔表示,德国政府希望最晚到2030年能在该国建成100万个充电桩。 作为传统汽车大国,德国在全球电动车蓬勃发展的大趋势下转型步伐显得滞后。德媒指出,德国政府此前设定的2020年左右电动车总量达到一百万辆的目标一再跳票,而应对气候变化的紧迫性亦给德国汽车业带来压力。 6 c; [1 b) `. _# F* L! B
4.罗永浩上了“老赖”名单
, Z, c2 M& c- f
8 T, F+ x% P/ W/ w$ V$ @) d9 J
/ R, i3 c9 H% g
11月3日下午消息,北京锤子数码科技有限公司及罗永浩被法院限制消费。
; T4 {/ n' M' d* K# f1 {
“彪悍的人生不需要解释。”这句话或能成为罗永浩的一个注解。从新东方英语老师,到砸西门子冰箱、质疑方舟子而名声鹊起,成为舆论领袖,创业前的罗永浩可谓顺风顺水。但自2012年宣布创业做手机以来,罗永浩接连遇到挫折,发布的几款手机叫好不叫座。今年再次创业的罗永浩看准了电子烟的风口,不想近期遭遇最严监管政策。
* Z/ b( v0 F9 ]4 _4 ?
11月3日晚间,罗永浩通过微博回应称,已还3亿公司债务;会继续努力,在未来一段时期把债务全部还完,哪怕以“卖艺”之类的方式。 0 ]9 \* @& P0 y! z! E, {
5.熬夜变傻有科学依据:科学家称睡眠时间大脑会开启“自动清洗”( y! Y7 Y7 o9 p$ K( s- U
) z; L) e1 W$ \
( ]7 j& r- A2 Z, M% J. F) z9 h( b
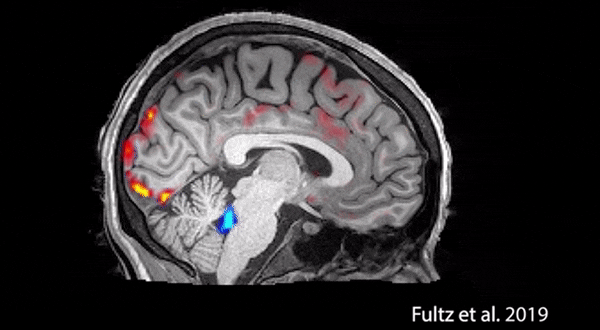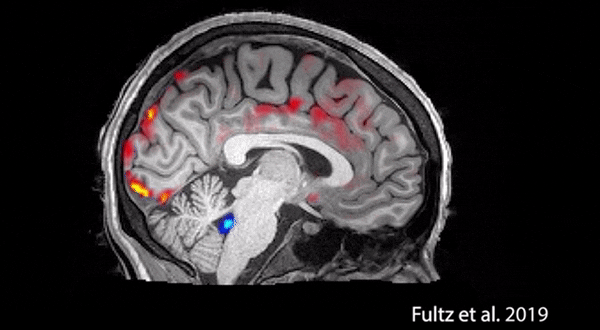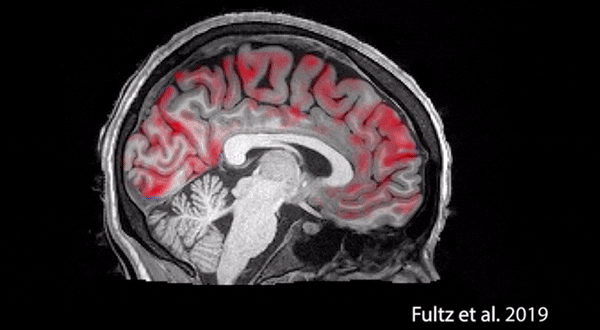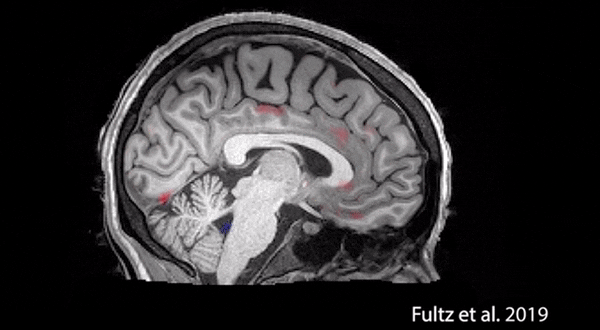
据据外媒报道,,波士顿大学的科学家们通过实验证实了睡眠的“清洗”作用。 : {% `( u9 a+ C
据悉,科学家们拍下了大脑自身清洗的过程,其中红色是血液,蓝色是脑脊液。血液会周期性地大量流出大脑,脑脊液趁机涌入,清除毒素。科学家表示,睡眠期间,神经元会同步活动,使大脑的血氧浓度出现周期变化。而醒着的时候,神经元不会同开同关,也就导致无法让大脑血量下降到足够低的水平。因此这样的清洗,只有睡着后才能做到,否则脑脊液没法趁虚而入。被清除的毒素包括β-淀粉样蛋白,而这正是导致阿尔茨海默氏症的一大元凶。 " m8 v7 O7 D- d* @% e
镁客网 2 n) F1 t+ f" `4 H2 k
9 V8 u( S/ w/ @" g1 Z& R2 x. Y8 W |